MAT.APLIC

Total de visitas: 5484

MAT.APLIC

Docente: João Raimundo

Objectivos da disciplina:

Desenvolver a capacidade de usar a Matemática como instrumento de interpretação e intervenção no real;

Desenvolver a capacidade de reconhecer regularidades e modelos matemáticos relevantes em cada aspecto da realidade, e de os utilizar para ajudar a resolver problemas, eventualmente em diálogo com especialistas;

Desenvolver as capacidades de formular e resolver problemas, de comunicar, assim como de memória, de rigor, de espírito crítico e de criatividade;

Utilizar os conhecimentos matemáticos na resolução de problemas, decidindo sobre a

razoabilidade de um resultado e sobre o uso, consoante os casos, de cálculo mental,

algoritmos de papel e lápis ou instrumentos tecnológicos;

Promover o aprofundamento de uma cultura científica, técnica e humanística que constitua suporte cognitivo e metodológico tanto para a inserção plena na vida profissional como para o prosseguimento de estudos;

Contribuir para uma atitude positiva face à Ciência em geral, reconhecendo o seu papel no progresso e desenvolvimento social e material, ao mesmo tempo que reconhecem a

necessidade do desempenho de cada um na manutenção e desenvolvimento dos sistemas;

Promover a realização pessoal mediante o desenvolvimento de atitudes de autonomia e solidariedade;

Criar capacidades de intervenção social pelo estudo e compreensão de problemas e

situações da sociedade actual e, bem assim, pela discussão de sistemas e instâncias de decisão que influenciam a vida dos cidadãos, participando desse modo na formação para uma cidadania activa e participativa.

O que mais gostei de saber:

Geometria Intuitiva.

1. Realização de atividades de investigação de geometria no plano e no espaço como forma de diagnostico e recuperação de conceitos geométricos básicos-trabalhar os políminos ou os polidiamantes (construções realizadas com quadrados e triângulos equilateros unidos pelos lados, respetivamente).

Das equações aos números.

1. Resolução de problemas que recorram a equações do 1º grau e sua resolução usando a reciprocidade das equações e as operações simples com polinomios.

2. Extensão do conceito de número aos racionais relativos.

3. Operações com números racionais elativos nas suas diferentes formas.

4. Resolução de problemas que envolvam sistemas simples de equações a duas incógnitas

Do plano ao espaço.

1. Transformações geométricas:ampliações, reduções, isometrias.

2. Semelhança de figuras, relações entre comprimento, áreas e volumes.

3. Rectas e planos: paralelismo e perpendicularidade.

Estatisticas e probabilidades.

1. Medidas de tendência central: média, moda e mediana.

2. Distribuições de frequências. Comparação de distribuições.

3. Espaço de resultados de experiências aleatórias.

4. Classificação de acontecimentos.

5. Probabilidade de um acontecimento como quociente entre casos favoravéis e casos possíveis.

6. Definição frequencista de probabilidade.

7. Escalas de probabilidade.

O que mais gostei de fazer:

Diversos tipos de gráficos estatísticos:

Gráfico de barras:

Gráfico é a tentativa de se expressar visualmente dados ou valores numéricos, de maneiras diferentes, assim facilitando a compreensão dos mesmos. Existem vários tipos de gráficos e os mais utilizados são os de colunas, os de linhas e os circulares. Os principais elementos são: números, título, fonte, nota e chamada.

Histograma:

O histograma é um gráfico composto por retângulos justapostos em que a base de cada um deles corresponde ao intervalo de classe e a sua altura à respectiva freqüência. Quando o número de dados aumenta indefinidamente e o intervalo de classe tende a zero, a distribuição de freqüência passa para uma distribuição de densidade de probabilidades. A construção de histogramas tem caráter preliminar em qualquer estudo e é um importante indicador da distribuição de dados.

Gráfico circular:

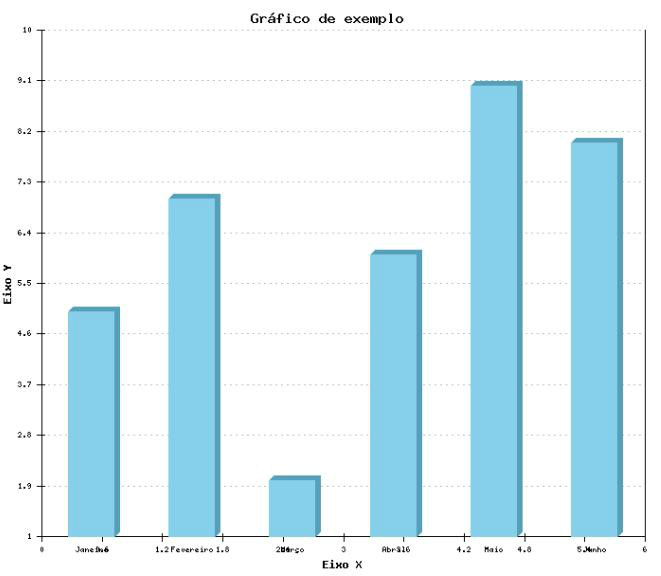
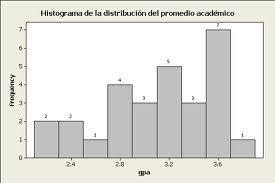
Representação gráfica da frequência relativa (percentagem) de cada categoria de uma variável. Este gráfico é utlizado para varíaveis nominais e ordinais. É uma opção ao gráfico de barras quando se pretende dar ênfase à comparação das percentagens de cada categoria.

Características:

a área do grafico equivale á totalidade de casos (100%)

cada 'fatia' representa a percentagem de cada categoria

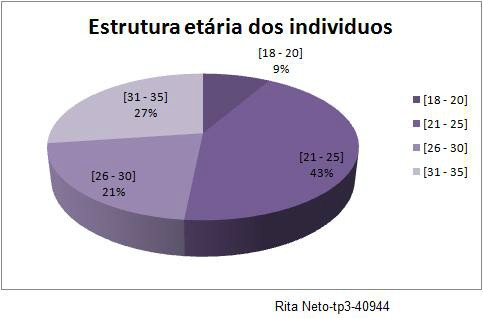
Gráfico de frequência relativas:

Frequência e Tabela de frequências:

A frequência absoluta, ou apenas frequência, de um valor é o número de vezes que uma determinada variável assume esse valor. Ao conjunto das frequências dos diferentes valores da variável dá-se o nome de distribuição da frequência (ou apenas distribuição).

A frequência relativa, é a percentagem relativa à frequência.

A frequência acumulada de um valor, é o numero de vezes que uma variável assume um valor inferior ou igual a esse valor.

A frequência relativa acumulada, é a percentagem relativa à frequência acumulada.

A tabela de frequências é uma forma de representação da frequência de cada valor distinto da variável. Juntamente com as frequências, esta poderá incluir frequências relativas, frequências acumuladas e frequências relativas acumuladas.